Oversampling In Distortion Effects

Loyal readers of The Science of Sound know I’m not a friend of super-high sampling rates for audio recording. But there are a couple of DSP processes that benefit from oversampling.

I know the debate will probably never end. Someone will always call for highest-possible sampling rates to ensure high quality audio. Audio equipment manufacturers will keep happily going for the low hanging marketing fruit of increasing sampling rates so the numbers on the box are higher than the competition’s.

And I’ll keep repeating that there’s no evidence whatsoever for higher sampling rates being of any benefit for audio recordings. Of course, given the audio converters used are well designed for use with standard sampling rates of 44.1 or 48 kHz. That’s a whole different story though. Even if some converters may perform better when running at double or triple sampling rates, they do so at the cost of (unnecessarily) wasting precious resources.

Oversampling

But that’s only valid for recording and playback. As soon as digital signal processing is involved, the rules change. Or to put it more precisely, the rules need to be applied more rigorously. I’m talking of the sampling theorem here of course.

Many signal processing algorithms require some care with respect to the sampling rate. Often, increasing the sampling rate during processing is a suitable strategy to avoid typical problems. This process is called oversampling.

Today I’d like to start a little series about basic DSP processes that benefit from oversampling. In this first installment of the series, we’ll talk about distortion effects, which we find most prominently in the context of guitar effects and amplifiers.

What Is Distortion?

Distortion in the purest sense means that the audio signal’s amplitudes are shaped using some mathematic function. In electronic circuits, this is due to nonlinear parts such as transistors or tubes. In practice, this usually occurs in combination with some filtering or similar processing. But in this context, I’d like to concentrate on the nonlinear shaping of the signal itself.

Practical distortion effects typically include some kind of clipping. That means that the signal amplitude can’t exceed a hard limit. If you push it really hard, you can turn a sine wave into a square wave.

Bandwidth Extension

The important thing to understand about this process is that it creates an extension of signal bandwidth. That means that distortion adds multiples of the frequency components of the original signal. So far so obvious, it’s pretty easy to hear.

Strictly speaking, distortion adds an infinite amount of signal bandwidth in practical cases. But the additional overtones decay towards higher frequencies, so at some point they disappear into the noise floor. Thus, we could quantify the bandwidth of the resulting signal somehow.

Aliasing

With a little knowledge about the sampling theorem, you know that bandwidth is absolutely critical. Any part of the signal spectrum that’s beyond half the sampling rate – the so called Nyquist frequency – will screw us big time.

For frequencies exceeding this limit, the Nyquist frequency acts like a mirror, reflecting everything higher than that back into the frequency range below. As if that’s not enough, when the “mirror image” reaches 0 Hz, it is reflected there again. This is known as “aliasing”.

We’ll get this problem if we distort signals so much that the new overtones exceed the Nyquist limit. Here’s an illustration:

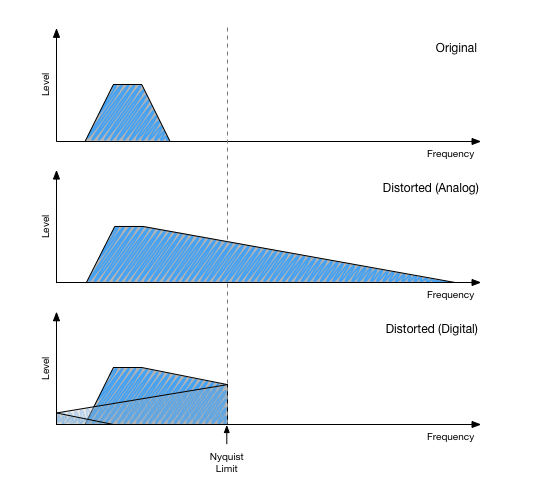
The first graph shows the spectrum of the original signal. The second one is the distorted signal as it would be in the analog domain, so without aliasing.

The dashed line represents the Nyquist frequency of our digital system. We assume that the sampling rate is chosen so that anything above the limit is inaudible anyway. So we don’t hear it, but it’s there.

The third graph shows what happens if we apply the distortion in digital domain. All content exceeding the Nyquist frequency folds back towards lower frequencies. And at 0 Hz it folds again. Digital origami.

The problem is best heard when bending high notes. You’ll then hear some “false” tones that bend up when you bend down or vice versa.

Anti-Aliasing

So what can we do about it?

It’s perfectly possible to deconstruct the distortion process mathematically and modify it so that it obeys to the sampling theorem and doesn’t create any content above the Nyquist limit. But honestly, that’s very expensive and it doesn’t work very well with extreme distortion. So in practice that’s not a viable solution, and I haven’t seen those techniques implemented outside of academic papers.

The most effective method is – you guessed it – oversampling. The sampling rate is massively increased before the actual distortion. This way we get a much larger frequency range to accommodate the overtones that the distortion creates. Then we can filter these out and convert back to the original sampling rate.

The required amount of oversampling depends on the amount of distortion. For only slight distortion, you can sometimes even get away with no oversampling at all. High-gain guitar distortion as the other extreme requires at least 16-32x oversampling to bring aliasing down to reasonably inaudible amounts. That’s a sampling rate of nearly 1.5 MHz!

But enough talking, here’s an example for you to listen to, courtesy of my limited guitar skills. It’s just a high bended note with heavy fuzz-ish distortion. The first one is without oversampling, the second one with 32x oversampling. And both repeated a second time. This is probably NSFW.

Listen most closely to the start of the tone and the weird artifacts that sound a bit like finding a station on an old radio. With oversampling, it disappears.

But on the downside, 32x oversampling results in 32x CPU load, plus the overhead for the oversampling, which itself is a process that requires some compromise in quality vs. cpu load.

Conclusions

Heavy distortion effects require extreme oversampling to avoid nasty aliasing artifacts. So this is one of the cases where the sampling rate can’t be high enough.

However, it is the algorithm designer’s responsibility to implement this and chose a reasonable compromise between sound quality and CPU load. Obviously, with such extreme sampling rates, it is reasonable to keep the oversampled processing to a minimum.

You can easily test your digital guitar effects by bending very high notes and listening for “radio noises”. Go ahead and try it out. And don’t forget to share your results in the comments!