Understanding Time-Frequency Segmentation
Humans are great at identifying, localizing and separating different sound sources in a complex mixture, like music. The key to sound source separation is time-frequency segmentation. Sounds great, huh? Let’s shed some light on these buzzwords.
Very recently, I wrote about the basic mechanisms that human hearing uses for sound localization. That’s all very fine and intuitively understandable in the case of single sounds. But usually we don’t have single sound sources in music, and neither in real life.
Sound Source Separation
In practice, we have to deal with complex mixtures of all kinds of sounds. Speech and singing, melodic and percussive instruments, and lots of noises. Human hearing has a remarkable ability to analyze these complex scenes. We can even direct our focus to specific sources inside the mixture and suppress others to a certain extent.
Sound localization plays a key role in this process in identifying different objects. But before that is even possible, our hearing needs to chop up the audio into small pieces. These small pieces can then be individually analyzed, grouped and sorted by importance before the information is made available to cognitive stages further down the road.
The key mechanism that makes this processes is called time-frequency segmentation.
What Is Time-Frequency Segmentation?
What this essentially means is that the auditory system periodically analyzes short time frames of audio for their frequency content. By doing that again and again, we chop up audio in two dimensions: time and frequency.
Chances are good you have seen similar representations before in the shape of so-called spectrograms. Many analyzer softwares offer that kind of view, where sound energy is shown across the two dimensions of time and frequency. Here’s one of a short speech sample:
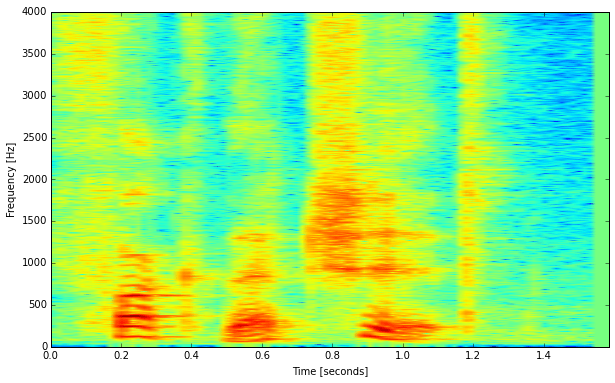
The time axis goes from left to right, and frequency spreads out on the vertical axis.
You can see the harmonics of the tonal components as comb-like groups of horizontal lines (especially around 0.2-0.4 seconds). Additionally there are also some transient events that occur like vertical lines, for example at 1.2 seconds.
Such a visualization is very useful because it is similar to what our ears actually generate and present to The Great Pattern Matching Machine (our brain).
The Dreaded Uncertainty Principle
The resolution of such a representation is limited, obviously. Even more, the resolution across the two axes of time and frequency depend on each other.
Intuitively it’s clear that the length of the analyzed time frames will affect the resolution in time. If you take longer time frames, you can’t take as many. So longer time frames result in coarser time resolution.
But the length of time frames also affects frequency resolution. Increasing the frame length increases the frequency resolution by the same amount.
As a result, there is always a tradeoff between the two. Better frequency resolution inevitably results in worse time resolution. Getting better at separating different tones means getting worse at separating different percussive events.
The image above shows a spectrogram with a rather high frequency resolution where we are able to see the harmonic partials of the tonal speech segments. This one here is made with a much shorter frame length and thus with a coarser frequency resolution:
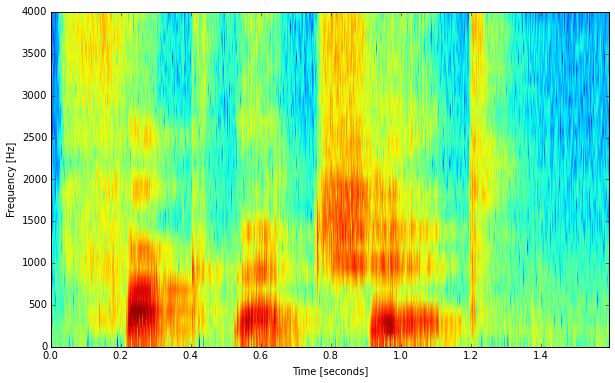
Note that the tonal segments look totally different now. You can’t see the harmonic partials anymore, but instead, you can almost see a series of vertical lines. These are actually the individual impulses that the vocal cords emit. Also, the transients that were already visible in the first spectrogram are a bit sharper here.
This is called the uncertainty principle of the Fourier transform. It does not apply only to the Fourier transform, but to any type of frequency analysis in one way or another.
Why is that? Well, if we want to be able to identify for example a sine wave of a certain frequency using only a limited time frame, at least one or more periods of the sine wave should fit into the time frame. The lower the sine frequency, the longer its period. So the longer the time frames must be to accommodate a big enough portion of a sine wave to recognize it as such.
Varying Uncertainty
The above examples were created using a Fast Fourier Transform. With this method, the frequency resolution is constant in all frequency ranges.
In human hearing, the segmentation in frequency domain happens mechanically inside the cochlea, as you learned in a previous article. But the frequency resolution of this process is not constant. At lower frequencies, it is much higher than at low frequencies. In fact, frequency resolution roughly doubles which each octave down.
As frequency resolution determines time resolution, the time resolution at higher frequencies is much finer.
Applying Sound Source Separation Principles In Music
In the practice of a musician or music producer, we usually don’t have to separate sound sources, except maybe for restoration purposes. In fact, we do the exact opposite all the time at the mixing stage.
So how could knowledge about sound source separation and time-frequency segmentation help us?
Modern music mixes and arrangements are very complex, with lots of different instruments and sounds playing together. Sometimes we need a surprisingly large amount of tracks to convey our message. The listener will have to decode it somehow.
Stereo and multichannel audio allow spreading the message in space, which helps a lot. But in order to present the listener with a well conditioned sound stage, it is vital to ensure that she can well distinguish all the different elements. The challenge is even bigger when listening in mono.
Mixing Advice
Common wisdom tells us that we should EQ different instruments so that they don’t overlap so much in the same frequency ranges. That certainly helps, but knowing what we know from the above paragraphs, it might pay to look a little closer.
Especially we should look at two dimensions instead of just one. We need to take the time domain into account, too.
So it’s usually no problem if different percussive instruments overlap in some important frequency ranges, as long as they don’t occur simultaneously all the time. Also it doesn’t necessarily hurt if percussion instruments overlap with a melodic or harmonic instrument, as percussion hits will still easily stick through.
More caution is advisable for percussion instruments with much low-frequency content. They can’t be separated as well in time domain as the high-frequency parts.
For different melodic or harmonic instruments, it is advisable to not have too much of them occupy the same higher frequency ranges. There, good frequency separation is key. In the lower mid frequencies, they can be separated better by their frequencies. But caution: due to their harmonic relationship, they will tend to overlap more anyway. Thus, the higher frequency resolution at lower frequencies is not that useful for clarity in a mix.
However, the bulk of the work around good separation takes place even before mixing. A good arrangement already takes care of most of the separation issues!
What are your tricks to get good separation in a mix? Can you relate them to time-frequency segmentation? Share your experience in the comments!

