About Sampling Rates in Digital Audio

We continue to dive into the foundations of digital audio. I hopefully cleared up a thing or two about the choice of bit depth already. And today I’d like to take you on a short trip into the unwieldy territory of the sampling theorem.

A source of constant debate in the world of digital audio is the choice of sampling rate. I have taken part in a lot of these debates myself, and in most cases I’d rather prefer the standard rates of 44.1 kHz or 48 kHz. As a DSP developer, I’m notoriously cheap on CPU cycles, and lower sampling rates obviously take up much less of this precious resource.

But there’s also the high-end bunch that would rather prefer working with 192 kHz all over the place. That’s understandable, because intuitively, more is better (except for the increased CPU load). However, this conclusion is mostly based on the misconception that sampling results in a coarse, stairstepped representation of a continuous audio signal. In reality, this is not the case. But fully trusting this requires understanding of the sometimes very counterintuitive sampling theorem.

In essence, a continuous signal can be exactly reconstructed from measurements taken at regular intervals (the sampling rate). With the limitation that the signal must not have any frequency content exceeding the so-called Nyquist limit or Nyquist frequency, which is at half of the sampling rate. Let’s take that for granted right now and first assume that this requirement is always fulfilled for the audio converters we use. The question would be then: which sampling rate do we need?

Chosing the sampling rate

As we did in the bit depth article before, we need to chose some kind of requirement we want to fulfill. This way we can find out which choice of sampling rate we would need according to that requirement. Again, the most reasonable choice is to look at the capabilities of human hearing. To chose a useful bit depth, we looked at the dynamic range of hearing and especially at the level of the softest sound we can perceive. Analogously, to chose a reasonable sampling rate, we need to look at the frequency range of hearing. Here’s a plot of the absolute hearing threshold, which is the lowest sound pressure level at which a sine wave of a given frequency can be reliably perceived by a healthy 20 year old person.

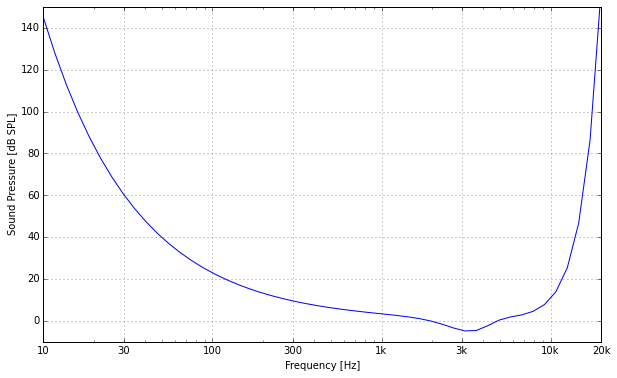
As we can see, there is a very steep rise of the threshold towards higher frequencies that starts at about 10 kHz. Although an often quoted ballpark number for the human hearing range is 20-20000 Hz, the levels required to perceive such frequencies are already quite insane. A more accurate number would be around 18 kHz. And over 30 years of age, the upper limit decreases even more. So in practice, the usual 20 kHz number does already include a bit of margin.

The lowest common sampling rate used in pro audio is 44.1 kHz, so this is theoretically enough to handle frequency content up to 22.05 kHz. All in all, using this standard CD sampling rate is around 4 kHz higher than would be needed in an ideal case, which gives us a nice security margin.

Possible artifacts

So far, we just assumed that the Nyquist criterion is fulfilled. But what happens if this is not the case? Well, if the original signal contains frequency content above the Nyquist limit, this content is effectively folded into the frequency range below this limit (this is a little shortcut to save you from a complete lecture on digital signal theory). That means that, if we have a sine wave at 30 kHz and sample it at a rate of 44.1 kHz without further countermeasures, the reconstructed signal would be a sine wave at 14.1 kHz. That is below the Nyquist limit by the difference between the original frequency and the Nyquist frequency. This phenomenon is called aliasing. Note that if we increase the frequency of the original sine, the aliased result decreases in frequency.

To avoid that, the original signal must be low-pass filtered before sampling it. This removes all signal components that would result in aliasing. In the earlier days of digital audio, this filtering had to be performed using analog circuitry in front of the actual converter, which always requires some margin due to the limited steepness of analog filters. Modern delta-sigma converters work differently. The conversion is done at a much higher sampling rate internally, but with only one bit resolution (information theory makes it possible to trade sampling rate and bit depth for each other). Then, most of the antialias filtering can be performed digitally, which is much more efficient. In this case, less margin is required in the analog domain.

Modern converter hardware is set up so that aliasing is not an issue, which essentially means that the level of any aliasing artifacts is below the noise level of the converter. The lowpass filters needed for that are very steep, so the slope of these doesn’t take up too much of the signal bandwidth. So far, it looks like with reasonably modern hardware, no sampling rate higher than 44.1 kHz or 48 kHz is needed for audio recording and playback.

But we barely scratched the surface yet. There are a lot more implications with the choice of sampling rate, especially when it comes to further processing. Also, we do not yet know exactly how our individual converter actually performs. In the future, you will learn more about how digital signal processing is affected by the choice of sampling rate. We’ll also investigate on the often debated question if it might be possible under certain circumstances to hear frequency content above the 20 kHz limit. And we’ll put our converters on the test bench, to see if they really hold their promises.

Have you tried using double sampling rates like 88.2 or 96 kHz for recording? Or maybe even 192 kHz? What are your experiences with that? Discuss in the comments!