How Does Oversampling Sound?
In the final part of the series about the ins and outs of oversampling, it’s time to look at the oversampling process itself and investigate how it affects the audio, even when no other processing is involved.
You know I like doing a series like this from time to time. It’s a good way to shed some light on different aspects. And spreading a topic over a couple of weeks gives an opportunity for the information to sink in. On a funny side note, most of the series I have done so far were a product of a totally failed attempt to cram all the information into a single article.
With the first three parts of this series I have concentrated on signal processing algorithms that may or may not benefit from being processed at very high sampling rates. By very high I mean much higher than the sampling rate needed to represent what humans can audibly perceive.
But so far, I left an important factor out of sight. We haven’t yet looked at how the oversampling process itself works after all.
The thing is, changing the sampling rate of an audio signal isn’t trivial at all. It does impose some unwanted effects on the audio. Depending on the actual implementation, this is true even if no processing is performed at all between up- and downsampling. That means, it’s not a transparent process.
So let’s look at how oversampling works in practice.
Oversampling Deconstructed
Obviously, oversampling is at least a two-step process. First the sampling rate is increased. Let’s call this process upsampling – or more precise: interpolation. The purpose of upsampling is to increase the sampling rate while preserving the original signal, and only the original signal.
After some signal processing is carried out at the increased sampling rate, the original sampling rate must be restored. This is done by the downsampling process.
As soon as the upsampled signal was processed in some way, decreasing the sampling rate again might not be trivial anymore. If the processing was nonlinear in any way, it will have added additional frequency content above the original Nyquist frequency. In order to satisfy the sampling theorem, the downsampling process must thus make sure that these frequency ranges are filtered out before decreasing the sampling rate.
But let’s get into detail a bit more…
Upsampling / Interpolation
You read above that oversampling is at least a two-step process. “At least” because the individual upsampling and downsampling processes also usually consist of two steps. You’ll see what these are in the following. But a word of caution, multirate signal processing is among the hardest topics to both understand and explain. So grab yourself a cup of coffee, you might use some increased attention here.
The important parts to distinguish in the upsampling process are the increase of sampling rate itself and the interpolation. Say you want to beef your signal up to 4x the original sampling rate, you need to insert three new samples between each original sample. But what are the numbers that should go there?
These numbers you get by using an interpolation algorithm of your choice. But first it’s a good idea to look at what it means to use no interpolation at all.
Increasing the sampling rate without any interpolation means the samples you are inserting are all zero. This way, no additional information or “energy” is added or removed to or from the signal.
If you look at the frequency spectrum of such a “zero-stuffed” signal, you’ll see that it has frequency content all over the place, not just up to the Nyquist frequency of the original signal at the lower sampling rate. In fact, the frequency spectrum is periodic with the old sampling rate. So in case of a CD, you’ll see the same frequency content every 44100 Hz. These additional images are called “aliases”.
See the following illustration to get an idea about what that looks like:
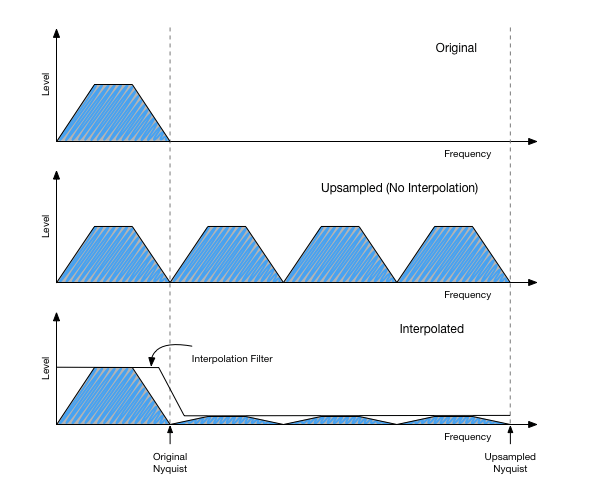
Ideally, all these alias images should be removed by the interpolation process. So every interpolation algorithm is essentially a filter that processes a zero-stuffed signal. In practice however, it is inefficient to do exactly that. Instead, the in-between samples are computed directly “before insertion”.
Downsampling / Decimation
Now let’s turn around and go back to our original sampling rate. You’ll see that the process is very similar.
Again, we can view the decrease of sampling rate without further processing separately. In our 4x oversampling example, that would mean keeping only one sample out of every group of 4.
It’s probably best to revive the illustration again that you know already from the first part of this series:
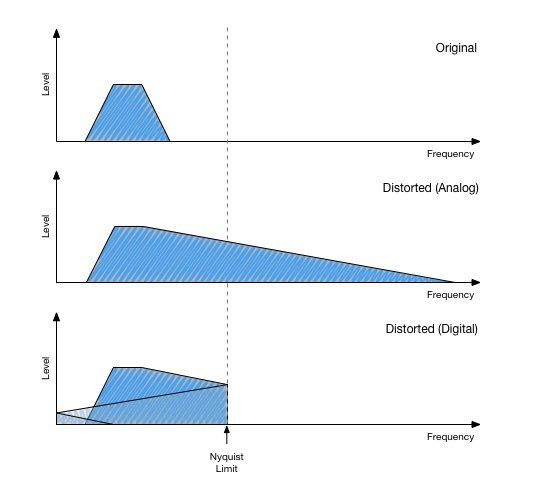
The upper graph shows the signal without distortion processing. If we ideally interpolate it to 4x sampling rate, it should look exactly like this. We could downsample to the original sampling rate again without further problems, because there is no content above the original Nyquist frequency.
But after distortion, the bandwidth is extended. If we remove 3/4th of the samples in that signal, the result would look exactly like the bottom graph. The spectrum folds around to fit into the new narrow frequency range.
So in order to safely decrease sampling rate, the content above the lower Nyquist frequency must be filtered out. The requirements for this filtering are the same as for the interpolation case.
In efficient implementations – again – both filtering and “sample removal” are combined into one step. This way, you avoid computing samples that you throw away afterwards anyway.
But how does it sound now?
OK, the point of the above is to make clear that everything comes down to the quality of the filters used. And any interpolation or decimation method that doesn’t look like a filter in the first, is in fact one nevertheless. For both upsampling and downsampling, the requirements for these filters are the same.
Ideally, such a filter would change absolutely nothing in the lower frequency range up to the original Nyquist frequency (let’s call this the pass band) and remove absolutely everything above that limit (the stop band).
Such a perfect rectangular filter frequency response is – unfortunately – impossible to implement in the real world. It would need to know the history of the signal right back to the big bang, and the complete future of the signal up to the next big bang. Thus, it’s a purely theoretic construction.
Any practical method will introduce some kind of compromise, such as:
- Letting through a certain amount of content in the stop band (affects aliasing rejection)
- Allowing a not perfectly flat frequency response in the pass band (affects transparency)
- Allowing the transition between the pass band and the stop band to be a bit broader (also affects transparency)
As always, all these quality compromises are also a matter of computational complexity. Better properties always come at the price of increased CPU load, and in many cases also increased latency.
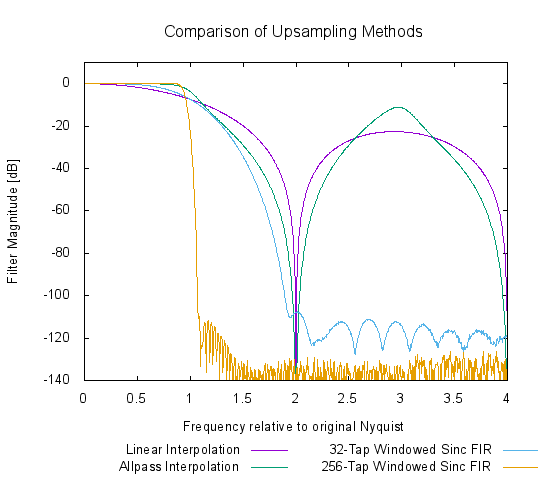
Let’s have a look at some different interpolation methods and their filter characteristics in the case of 4x upsampling:
Notice both the differences in stop band damping (everything above frequency “1”) and the different linearity in the pass band. Linear interpolation and allpass interpolation are very simple techniques with low CPU load and latency. As you can see, this comes at the price of very bad quality. The other two methods are both simple linear phase FIR filter designs with a different filter length. The longer the filter, the steeper it is. But that obviously comes at the price of much more CPU load and latency.
Conclusions
Wow, that was quite a ride! As I said above, multirate signal processing is a tough one.
If you have read through all this, you’ll be either totally confused because this was way over your head, or you feel some kind of academic anger because I explained some things a bit sloppily and contrary to the actual rigorous mathematical theory behind it. I might do another article about how all this stuff with aliasing really works true to the theory.
I don’t think there is the right way or tone to explain all this in short. But if this specific view on the topic has enlightened at least one or two people out there, I’m the happiest person on earth.
Apart from that, I invite you to the comments section of this article to discuss any questions. And I’m also always in for a little academic dispute. 🙂