Room Modes and Speaker Placement – An Intuitive Approach
Today we dip our toes into one of my favorite topics: room acoustics! In this article I’ll show you an elegant way of understanding the influence of room dimensions and speaker placement on room modes.
When researching audio topics, I am always looking for a simpler than usual way to think about it. Building that kind of intuition is the key to understanding problems and probably finding elegant solutions that wouldn’t be as obvious otherwise. One motivation for creating The Science of Sound is to build a platform to present and discuss these hopefully helpful mind tricks. And this is one of them.
It is a well known fact that the placement of speakers in a room and the listening position can greatly affect how sound is perceived. The frequency response from speaker to listener varies greatly with their respective positions.
The way this is usually explained in textbooks is by solving acoustic wave equations for a rectangular room and showing graphs of sound pressure distribution. The problem is that these solutions usually don’t take into account where the speakers and/or listeners actually are inside the room. Also, the direct path from loudspeaker to listener is ignored this way.
There are also room mode calculators all over the internet that help you predict at which frequencies room modes might occur, but they aren’t very useful in order to get a realistic picture. The only reliable way is to measure. Luckily, there are some great tools out there today, even free ones, like Room EQ Wizard.
However, it always pays off to have a certain level of understanding what’s going on, and that’s where models come into play. And a model always starts by greatly oversimplifying reality. But it helps, so let’s do it!
A One-Dimensional Waveguide Model of Room Modes
What we’ll do now is to create a simplified model of one room dimension. This represents how sound waves travel either back and forth, left to right or bottom to top inside a rectangular room. This is equivalent to what room mode calculators call axial modes. But here we incorporate the position of the loudspeaker and the listener. This is what it looks like:
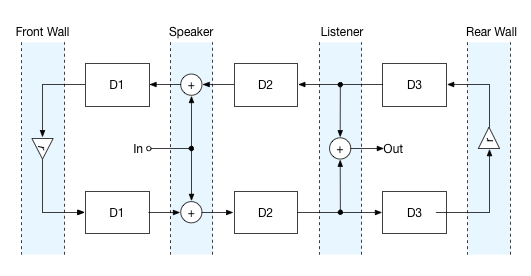
You read it like this: the rectangles represent delay times due to the propagation of sound waves through the air in the room. The loudspeaker emits sound waves both towards the listener and towards its rear. At the bottom, the sound travels towards the listener and passes on to the rear wall. There some of it is reflected, represented by the reflection coefficient r. The reflected sound travels in the opposite direction and passes the listener again. Further down the road, it passes the loudspeaker. There, the sound that the speaker emits to the rear direction is added to the wave that is already in the room. Traveling on, the sound waves are reflected again and travel on in the opposite direction. And so on, and so on.
Thus, D1 represents the time it takes for sound to travel from the loudspeaker to the front wall, D2 from loudspeaker to listener, and D3 from listener to rear wall.
For simplicity, the walls in this example reflect sound in the same way independently of frequency. Also, both loudspeaker and listener are omnidirectional, which means they emit or receive sound in the same way, independent of direction or frequency. More realistic conditions could be added without a problem, but that would obfuscate what we’re onto right now.
Keep It Simple, Stupid
Now the model above is probably quite intuitive to understand. But it’s still hard to see what the actual results are. Luckily, linear system theory allows us to rearrange and combine elements to get an absolutely equivalent structure that is much easier to analyze. This structure here is actually exactly the same as the above:
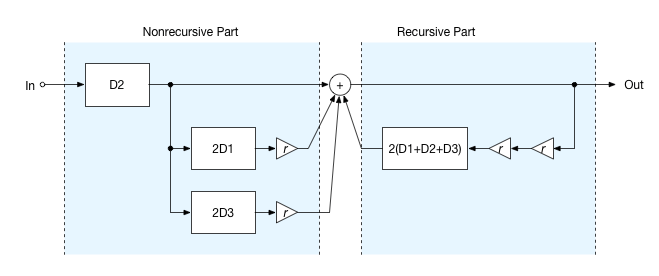
I have to omit the individual steps that lead from A to B here, but if you ask really nicely in the comments, I might make some more drawings.
The cool thing here is that now the complicated model that we were looking at falls together into much simpler building blocks. The first stage is the obvious distance from loudspeaker to listener. Added to the direct signal path are single reflections from the front and rear walls.
After that follows a recursive part that describes how sound travels back and forth through the room, damped by absorption. This is what actually creates room modes!
To loyal readers of The Science of Sound, these individual structures might look familiar. What we see here is a combination of feedforward and feedback comb filters!
What We Can Learn From It
So what does this structure actually sound like? Take a look back at the article about comb filters.
The feedforward part leads to sharp notches in the frequency response. The stronger the reflections from the walls, the deeper the notches. The frequencies of the notches depend on the positions of loudspeaker and listener. This is the part that you can influence by moving the loudspeakers and your chair around.
The feedback part in turn leads to sharp peaks in the frequency response. The interesting thing is that these peaks are always there, no matter where you are, no matter where the speakers are. The only way to influence this part (without altering the room dimensions) is by changing the reflection coefficients using absorbers.
However, if we place the loudspeakers so that some of the position-dependent notches overlap exactly with peaks caused by the room dimensions, we might compensate for some room modes a little bit. But that’s probably hardly possible in practice.
A more practical advice that can be derived from this model is to either place monitors directly at the front wall to achieve a near-zero reflection delay, or as far away from the front wall as possible to maximize the reflection delay so our ears can properly filter it out. That’s also what most loudspeaker manuals propose.
But in fact, it’s probably too early to derive advice on loudspeaker positions from this model just yet. There are too many additional factors involved that this model obviously doesn’t incorporate. For now, the goal is to convey a certain way of thinking about what happens to sound in a listening room.
I’ll let that sink in for today. As always, please post any questions and additional thoughts and experiences in the comments!
