Making Phase Audible – Part 3: Comb Filters
And on we go to the third and final part of the series about making phase audible. This time it’s about the most important ways in which a phase response influences sound tremendously. At the same time, I’m introducing a highly versatile concept that will become a recurring theme on The Science of Sound.
But before we get into the weeds, let me shortly recap why I treat this topic so deeply. The purpose of this series of articles is to help you build an intuition about how different types of processing can affect the audible results. The thing is, there is a good reason that most of the time when talking about audio processing, we are talking about magnitude responses, because that’s what we hear mostly.
As I stated in the introductory article to this series, confusion usually arises when phase comes into play. Not surprisingly, given that phase is an aspect we mostly don’t hear directly (as seen in part 1 of this series). Fascinatingly, my observation during many many conversations is that “phase” is often used as a buzzword to accommodate any phenomenon that can’t be clearly identified or named otherwise.
“Phase” is often used as a buzzword to accommodate any phenomenon that can’t be clearly identified or named otherwise.
What I want to do here is to help you build an intuition about audio processing that enables you to discern and identify different basic building blocks of audio processing. This helps with breaking down complex phenomena into smaller more manageable pieces. By combining knowledge about these building blocks, complex systems can be understood more easily.
But let’s now go by looking at two cases that we encounter all around us, all the time. I’m talking about comb filtering in it’s various forms. We can describe a lot of audio phenomena – especially in room acoustics – as combinations of two basic comb filter structures. The feedforward and feedback structures.
Feedforward Comb Filter
The structure is probably best described in a picture. This is the typical form of a feedforward comb filter:

Here the output signal from some kind of (yet unspecified) phase response is mixed with a copy of the input signal. Both signals will add up either constructively or destructively depending on the phase response. At frequencies where the phase response is a multiple of 360 degrees, we have constructive interference, so these frequencies will be doubled in magnitude (that is a boost of +6 dB). Destructive interference happens everywhere the phase response is 180 degrees (plus multiples of 360 degrees), which means silence.
If you look at this magnitude response of a comb filter with a delay of 10ms (= linear phase response), you get a harmonic series of peaks with the notches between them. The peaks are at multiples of one divided by the delay time in Hertz. If you reverse the polarity of one of the signals, peaks become notches and the other way around.

In this case, the peaks and notches are distributed in harmonic intervals because the phase response is linear (a peak every 100 Hz). When we instead insert a non-linear phase response, such as a chain of allpass filters, the intervals become non-harmonic.
You most probably know these effects already, as this is how choruses, flangers and phasers work. Choruses and flangers use short delays, while phasers use a chain of allpass filters. In all cases, the audible effect is achieved by mixing with the direct signal. Additionally, the delays/allpasses are also modulated.
Besides modulating the comb filtering effect to make more interesting, the modulation at the same time leads to a certain amount of vibrato, as we learned last week.
Feedback Comb Filter
There is a second type of comb filter as well that has a similar effect. You get it if you feed the output of a phase response back into the input. Like this:
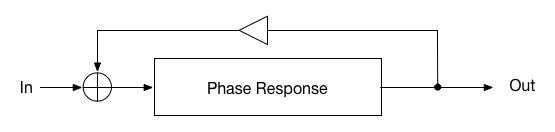
Obviously, if you feed the full signal back the result will continue infinitely, which is usually not what we want. Consequently, the damping coefficient represented by the triangle in the picture is very important for this type of structure. The more the feedback signal is dampened, the shorter the output will ring after the input signal is gone silent.
It’s interesting to compare the magnitude response of this structure with that of the feedforward comb filter, both with a 10ms delay. Look at this plot:
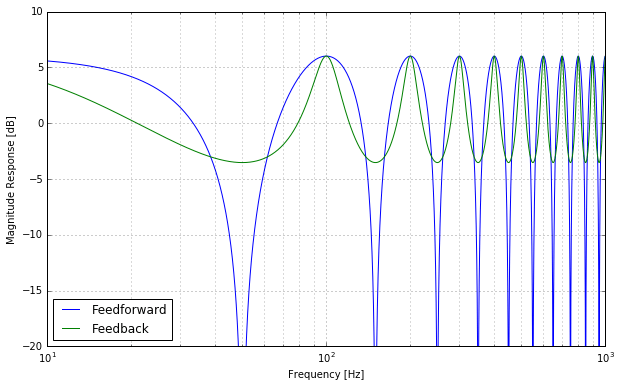
In this case the feedback factor is 0.5, which makes the peak amplitudes equal to the full feedforward case. You see that the shapes of peaks and notches are effectively exchanged. Instead of wide peaks and narrow notches, we now have narrow peaks and wide notches.
Also, the depth of the notches is now limited while the peaks will become higher and higher if you increase the feedback factor. At full feedback, the peaks become infinitely high while the notches will reach their limit at -6dB. Increase the feedback even more and the whole thing will explode (it becomes unstable).
So in many regards, the feedback comb filter is exactly the opposite of the feedforward one. And that’s also true if you again replace the trivial delay with an arbitrary phase response.
By the way, some implementations of the aforementioned effects also let you add a feedback to get a more resonant and peaky sound.
Comb Filters Are Everywhere
OK, you might think now “oh I get it, so that’s the complicated way of explaining phasers and flangers?”
It is, but there’s much more to it. The important thing to understand is that these two comb filter types and combinations thereof are literally all around us!
Look around your room. There are surfaces everywhere that reflect sound. All of them creating little feedforward comb filters. But the reflections in turn get reflected back and forth, especially at parallel walls. These are feedback comb filters (and very very complex combinations of those).
The feedback parts depend only on the shape of the room itself and the materials it is built from. The feedforward parts on the other hand, are highly dependent on where you place the speakers and where you sit. Thus you can change the feedforward part (with its nasty deep dips) easily by moving stuff around. To alter the feedback characteristics (the dreaded peaky ringing), you need to change your room geometry and absorption characteristics.
Another example is almost every acoustic instrument. You can for instance model any string (like that of a piano or guitar) as such a comb filter structure. Vibration travels along the string and gets reflected back and forth at the bridge and neck respectively, which clearly forms a feedback loop.
The time it takes for the vibrations to complete such a loop determines the pitch that you hear. But there’s also a feedforward component through both the position of the pickups and the position where you pick the string, which alters the overall weighting of different overtones.
The same goes for any acoustic instrument, such as wind instruments and even drums. You always have a feedback component (or an awful lot of them) that determines the tone, and a feedforward component that further shapes the timbre.
Adding to that, with real metal strings, string vibrations don’t travel at the same speed at all frequencies (the phenomenon is called “dispersion”). Thus, the “thing in the middle of the comb filter” is not a trivial delay, but a nonlinear phase response. As a result, overtones are slightly detuned from a perfect harmonic series, which results in a slightly metallic tone. Church bells take this inharmonicity to the extreme.
That was just a glimpse on how important and fascinating these two structures are. Nearly every complex process in acoustics can be decomposed into a combination of feedback and feedforward comb filters. Having a solid intuition about how to play with these properties is a great skill to have, and we’ll continue to encounter this stuff in a lot of ways.
Photo credit: Dean Hochman via Foter.com / CC BY

