Understanding Negative Feedback
Today we dive a littler deeper into electronics and look at an important technique used to keep nonlinear distortion in check: negative feedback!
OK, I do realize that this sounds like there’s some horrible theoretic stuff in front of you. And there probably is. But bear with me. The reason I chose this topic is that it illustrates some important issues to remember when thinking about the nonlinear behavior of any audio device. And apart from the general frequency response, this nonlinear behavior is the most important source of what we usually call “character”.
Nonlinearity
The problem is that we can’t really get rid of nonlinearity in electronics. All the nice active components we need are strongly nonlinear. But there are a couple of tricks to make them behave in a nicer way.
For every nonlinear component and circuits involving such components, we can calculate the characteristics by which it translates input voltages to output voltages. This characteristic curve describes the distortion imparted upon the signal when it passes through the circuit. Ideally, this curve should be a straight line, in which case the transfer characteristics are perfectly linear.
In practice, there are basically two methods to get nonlinear components to behave in a more linear way. The first method is to operate the circuit at low levels compared to the shape of the characteristic curve. If you zoom in enough into any nonlinear curve, a small segment will look enough like a straight line. But of course reducing signal amplitude is a bit counterproductive, for example if designing a microphone preamp. Instead, the curve can be magnified by increasing supply voltages (which usually determine the outer limits of the curve).
Of course, increasing supply voltages makes everything bigger and more expensive, and it isn’t all that effective in the end.
A much more efficient method is the technique I’d like to explain today: negative feedback.
Negative Feedback Basics
So what’s negative feedback? It basically means that a portion of the output signal is subtracted from the input signal. But how would that help?
In essence, by adding negative feedback we create a control loop that permanently checks the output signal against our (linear) expectation. If the output voltage is “too low” due to the nonlinear components, the input voltage is amplified a bit more until everything is fine again. This control process happens in an instant with practically no delay.
But obviously, the negative feedback decreases the overall gain, because effectively the input signal is decreased if we subtract a scaled version from it. So for negative feedback to work, the gain of the amplifier inside the loop must be higher than the gain we want to achieve in the end. We’ll see in a moment what “higher” really means here.
Theory
Let’s get a bit closer to the theory. Here’s what such a negative feedback loop looks like:
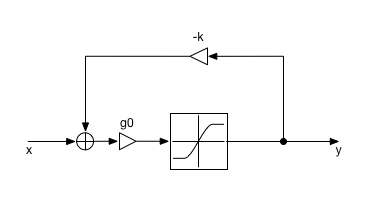
The box in the middle combined with the g0 multiplier before it is our highly nonlinear amplifier circuit, where g0 is its open-loop gain. The shape of the characteristic curve is already depicted in the diagram. For the following examples we use a tanh function as nonlinearity, which is the typical nonlinear characteristic curve of several common tube and transistor circuits.
You see that the output voltage is multiplied by some factor k and then subtracted from the input. It is this feedback factor that determines the actual gain of the complete circuit. That is, if g0 is sufficiently large compared to the desired gain. Then it has virtually no effect on the resulting gain.
If you write that down as a formula, this is the result:
y = \mathrm{tanh}(g_0 (x - ky))
Note that in order to compute the output voltage, we need to know it beforehand. Sounds impossible, but actually it isn’t like that. Physics don’t compute the same way we do with a pocket calculator. Think of it this way: for any x, there is one y that satisfies this equation. This is the output you get in the real circuit.
There are mathematical methods we can use to figure the solution to this equation out, and we’ll do that in a second. But first let’s try to find out more about k and g0.
If we assume for a second that everything is linear, we can find out that the resulting gain of this amplifier is
g = \frac{1}{\frac{1}{g_0} + k}.
If we make g0 really high, the term simplifies to 1/k. Thus, with very high open-loop gains, k alone determines the actual gain. This simplification holds for small signal amplitudes. For higher amplitudes, the signal get both distorted and compressed.
Practice
I coded a little something up to solve the impossible equation above numerically (yep, that’s the zero-delay feedback methods everyone keeps talking about). To better illustrate what happens I chose k so that we have a resulting gain of 1 (a so-called buffer). When g0 is increased, k is increased as well to keep the overall gain at 1. So what I actually vary here is the amount of “excess” gain that the amplifier has beyond the gain we want to achieve.
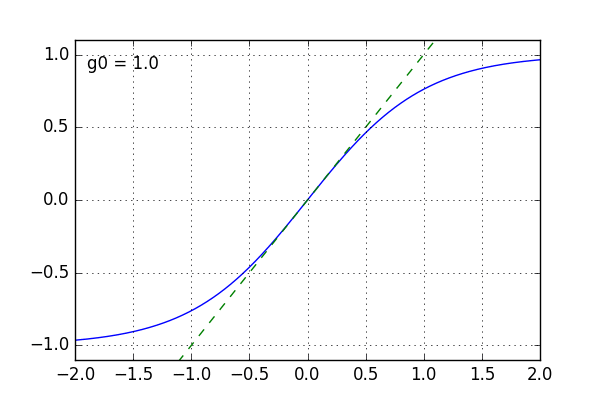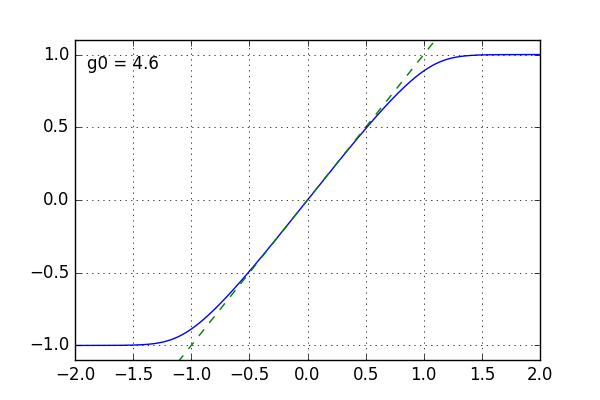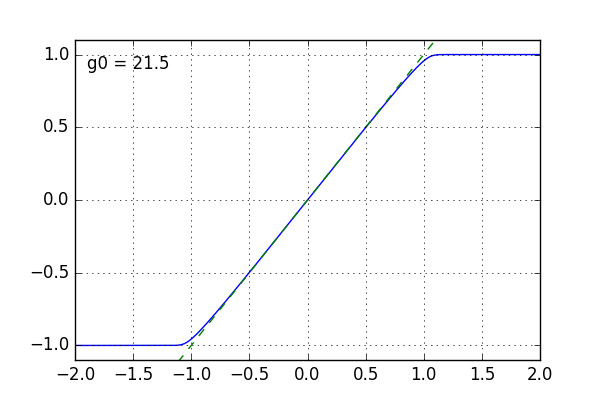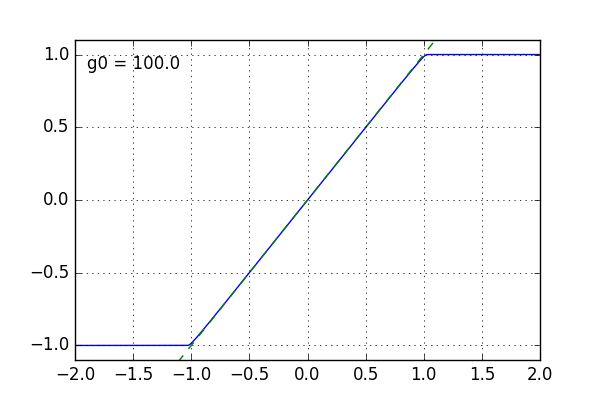
In this animation you see that as g0 is increased, the curve becomes more and more linear, the dashed line being the ideal curve. The clipping limits stay the same, as they are determined (mostly) by the voltage supply.
One important thing to notice here is that with more open-loop gain, the improvement when adding a bit more to it becomes lower. Perfect linearity is thus only achieved with infinite open-loop gain.
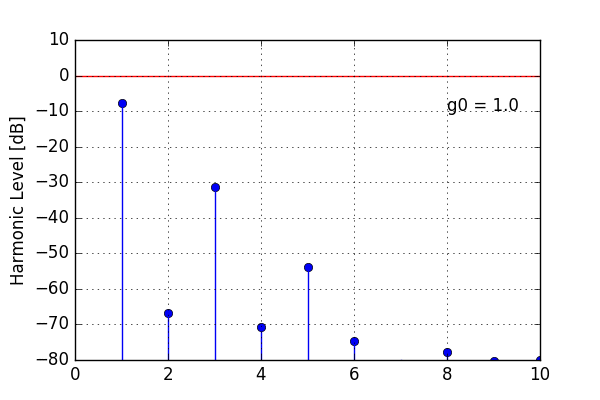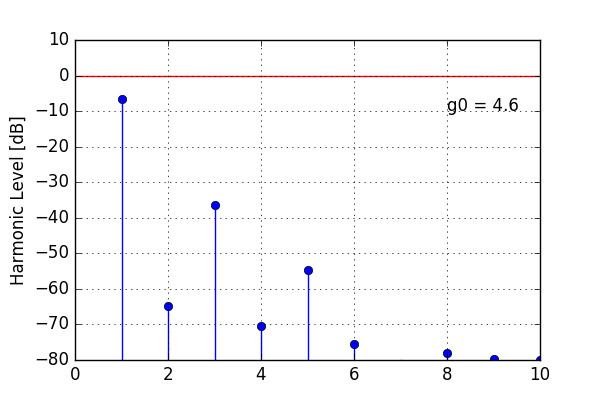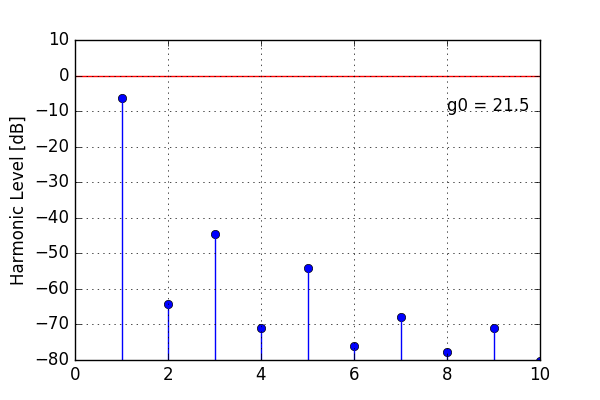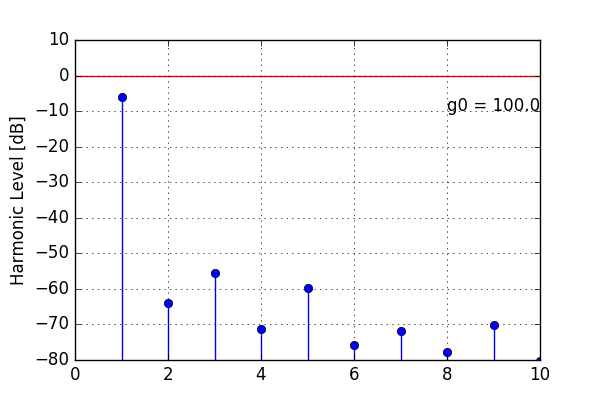
Here’s what happens to the spectrum of a full-scale sine wave. What you see is the first ten harmonic overtones that result from the nonlinear distortion. With increasing open-loop gain, the overtones decrease in level. But at g0 = 100, we still have harmonic distortion “only” around 60 dB down.
This concept of an amplifier with extreme gains combined with negative feedback is actually what is commonly known as an operational amplifier or opamp. This way we get an extremely versatile, linear, cheap and small component that we can do a whole lot of stuff with.
BTW: apart from just amplifying signals, we can also use frequency-dependent feedback to implement filters. For example we can increase the feedback for high frequencies to implement a lowpass filter. But that’s a whole different story.
What’s the consequence, after all?
The key takeaway here is that we need a lot of excess open-loop gain to get really clean results. It should be at least 40-60 dB higher than the actually desired gain. Typical opamps do provide such high gains. But only at very low frequencies. The gain starts to decrease often far below 1 kHz. So the higher the frequencies, the less excess gain there is, and the more nonlinear a circuit becomes.
This frequency-dependence of nonlinear characteristics is surprisingly rarely talked about. If at all, you might occasionally see a THD measurement at 1 kHz in a datasheet. THD being a notoriously useless value in itself, measuring it only at one frequency makes it even worse.
The thing is, what really determines the sonic character of a circuit is not so much the characteristic nonlinear curve itself, but much more how strong any nonlinear characteristics vary with frequency.
This is of course only one example for this phenomenon, and more will surely follow. Don’t forget to subscribe to the newsletter to follow along and grab a free plug-in while you’re at it!

